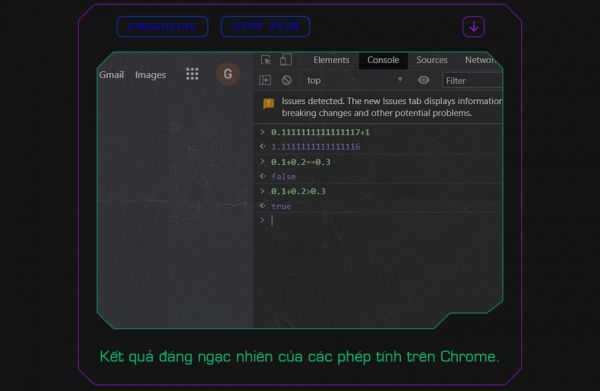
Có lẽ, các lập trình viên đều đã ít nhất một lần gặp phải các hiện tượng kỳ cục khi thực hiện phép tính trên các số thập phân. Ví dụ điển hình là Javascript, ngôn ngữ có vai trò cốt lõi với trải nghiệm web hiện nay. Bạn có thể thử nghiệm những phép tính kỳ lạ trên Javascript bằng cách mở Chrome, nhấn F12 (để mở công cụ cho nhà phát triển), chuyển sang tab console và gõ 0.1111111111111117 + 1. Kết quả bạn nhận được sẽ là… 1.1111111111111116.

Hay, bạn thử nhấn 0.1 + 0.2 == 0.3. Chrome sẽ trả ra kết quả là false, có nghĩa rằng 0.1 + 0.2 KHÔNG có giá trị bằng 0.3. Thử gõ vào 0.1 + 0.2 > 0.3 và bạn sẽ nhận kết quả true, có nghĩa rằng, với trình duyệt phổ biến nhất thế giới, tổng của 0.1 và 0.2 là một con số lớn hơn 0.3.

• THẾ GIỚI CỦA BÓNG ĐÈN

Để hiểu lý do cho hiện tượng "kỳ quái" này, trước hết chúng ta cần nhìn lại sự khác biệt căn bản giữa con người và máy tính. Với mười ngón tay (và mười ngón chân), con người quen với các phép tính thập phân, sử dụng 10 chữ số. Trái lại, máy tính sử dụng hệ nhị phân, nơi mọi giá trị đều được thể hiện bằng hai ký tự 1 hoặc 0, hay nói chính xác hơn là hai trạng thái của các bóng đèn/bóng bán dẫn: bật và tắt.

Thực chất, toàn bộ cuộc cách mạng điện toán, từ IBM PC cho đến MacBook Air, từ BlackBerry cho đến iPhone, từ Internet đến AI, tất cả đều bắt nguồn từ một khái niệm đơn giản: các bóng đèn bật/tắt có thể được sử dụng để biểu diễn và tính toán các giá trị nhị phân. Chiếc máy tính đầu tiên trong lịch sử loài người, ENIAC của Đại Học Pennsylvania nước Mỹ, có 18000 bóng đèn, nặng tới 27 tấn và chiếm diện tích tới 167m2.

Với phát minh vĩ đại sau này là bóng bán dẫn làm từ silicon, những cỗ máy chứa hàng ngàn bóng đèn bị thay thế bởi những con chip chứa hàng triệu bóng bán dẫn. Theo định luật Moore, máy tính ngày một thu nhỏ và mạnh mẽ hơn. Ngày nay, một con chip di động nhỏ bằng móng tay có thể chứa đến hàng tỷ bán dẫn: Snapdragon 865, Apple A13 đều có 8,5 tỷ bán dẫn, Exynos 990 và Kirin 990 có 10,3 tỷ...

Mỗi bóng bán dẫn này đóng vai trò (gần) giống như bóng đèn ngày trước: có dòng điện chạy qua là con số 1, không có điện chạy qua là số 0. Hiện tại, phần lớn các mẫu chip di động đã chạm tay tới quy trình 7nm: mỗi mm2 diện tích chip có thể chứa đến 100 triệu "bóng đèn" để tính toán.

• LÀM THẾ NÀO ĐỂ BIỂU DIỄN 0.5

Bạn có lẽ đã biết cách tính giá trị thập phân của các số nhị phân: từ phải sang trái, nhân chữ số (0 hoặc 1) với 2^0, 2^1, 2^2… rồi tính tổng. Ví dụ, "001" là 1, "010" là 4, "111" là 7. Nếu thêm một bit 0 hoặc 1 ở đầu tiên để đại diện cho dấu + hoặc -, chúng ta có thể dùng hệ nhị phân để biểu diễn cả số nguyên dương lẫn số nguyên âm

Vấn đề là ở chỗ, khi chỉ dùng 0 và 1 máy tính (hay con người) đều chỉ có thể tạo ra các số nguyên mà thôi. Làm thế nào để các bóng đèn của chúng ta khi bật và tắt vẫn có thể biểu diễn các chữ số sau dấu phẩy/dấu chấm, như 0.1 hoặc 0.1111111111111116 chẳng hạn? 

(Trong bài viết, chúng ta dùng dấu chấm thay cho dấu phẩy vì các phần mềm và các ngôn ngữ lập trình mặc định dùng dấu chấm).

Câu trả lời là một hệ thống biểu diễn số có tên "số thực dấu phẩy động". Trong hệ thống biểu diễn số này, các số thập phân có thể được biểu diễn dưới dạng S×2^e, trong đó cả số định trị S và số mũ e đều là số nguyên, có thể biểu diễn các ký tự 0 và 1. 

Cách biểu diễn này hoàn toàn tương thích với hệ nhị phân. Trên máy tính, mỗi giá trị số sẽ được thể hiện bằng nhiều "bit". Mỗi bit có thể hiểu là một "bóng đèn", có giá trị 0 hoặc 1. Khi có 64 bit chẳng hạn, máy tính sẽ dùng một số bit để lưu trữ số định trị, một số bit khác để lưu số mũ. Và khi S=1 và e là một số nguyên < 1 chẳng hạn, chúng ta sẽ tạo ra được những số thập phân có giá trị nhỏ hơn 1. Ví dụ 0.5=1*2^(-1), có thể biểu diễn với số định trị 1 và số mũ -1.

• GIỚI HẠN CỦA MÁY TÍNH SO VỚI CON NGƯỜI

Dựa vào công thức trên, bạn có thể hiểu vì sao máy tính sau hàng chục năm phát triển vẫn cho ra kết quả 0.1 + 0.2 > 0.3 và nhiều sai lầm tưởng ngớ ngẩn khác. Cả 3 con số này đều không thể biểu diễn hoàn toàn chính xác dưới dạng S×2^e. Thực chất, trong hệ nhị phân dùng dấu phẩy động, khi biểu diễn các giá trị > -1 và < 1, máy tính của chúng ta chỉ có thể biểu diễn chính xác các giá trị 1/2, 1/4, 1/8, 1/16, 1/32… và tích của chúng với các số nguyên mà thôi. 

Như 0.1 là 1/10, và do 10 không chia hết cho bất kỳ một lũy thừa nào của 2, các con chip nhị phân sẽ chẳng thể nào tạo ra số thực dấu phẩy động biểu diễn chính xác giá trị 0.1. Trong thực tế, điều này cũng xảy ra khi con người cố gắng thể hiện một số giá trị hữu tỉ trong hệ số thập phân. Ví dụ, 1/3 không thể nào thể hiện chính xác dưới dạng số thập phân x.y mà chỉ có thể là 0.333333… hoặc 0.(3), trong đó số 3 lặp vô hạn. Con số 1/10 khi thể hiện dưới dạng nhị phân dấu phẩy động cũng sẽ đòi hỏi một vòng lặp vô hạn, cụ thể hơn là 4 chữ số "1100" lặp vô hạn khi số mũ là -4.

Vấn đề là ở chỗ con người có thể hiểu được khái niệm "vô hạn", còn máy tính thì không. Kể cả có hàng triệu bán dẫn trên một con chip thì những giá trị máy tính ghi lại được vẫn là hữu hạn. Thực tế, các ngôn ngữ lập trình thường dừng ở mức 64-bit, tức là chỉ tạo ra các số nguyên có giá trị tối đa là 2^64 - 1. Con người biết đến sự tồn tại của tập số nguyên dương, tập số hữu tỉ, tập số thực… - vốn là các tập hợp vô hạn. Còn máy tính vốn suy nghĩ bằng những bóng đèn bật tắt - sẽ chẳng có tập hợp vô hạn nào tồn tại trong thế giới của chúng cả. 

Dĩ nhiên, các bóng đèn bật tắt thì cũng chẳng thể nào có khái niệm "1/10" bóng đèn. "Sống" trong hệ nhị phân, chiếc laptop Windows, chiếc iPhone hay smartphone Android của bạn cũng không hề có khái niệm 0.1 hay 1/10 hay số Pi... Chúng chỉ có thể dùng các bit 0 và 1 để biểu diễn các con số thập phân. 

Và điều đó đưa chúng ta trở lại với giới hạn cuối cùng, nặng nề nhất của máy tính. Các bóng đèn, bóng bán dẫn khi bật tắt sẽ chẳng thể nào biểu diễn chính xác số 0.1, thay vào đó chỉ có thể tạo ra số 0.100000001490116119384765625, vốn là 13421773 * 2^(-27). Một lần nữa, 13421773 và -27 đều là số nguyên, đều có thể biểu diễn bằng 0 và 1 trên bán dẫn.

• BẮT BUỘC PHẢI LÀM TRÒN

May mắn là, sự khác biệt giữa 0.1 và 0.100000001490116119384765625 nhỏ hơn 10^-9, và vì thế có bỏ qua. Chúng ta đã luôn bỏ qua "khiếm khuyết" này của máy tính để tạo ra những tựa game đẹp như trong mơ, những phép chẩn đoán ung thư chính xác hơn cả bác sĩ, những ván cờ đánh bại cả đại kiện tướng số 1 thế giới.

Vậy vì sao 0.1 + 0.2 lại cho ra kết quả 0.3? Lý do là bởi, 0.1 và 0.2 thực chất đều được máy tính làm tròn từ những con số lớn hơn giá trị thực của chúng, còn 0.3 thì lại được làm tròn từ một con số nhỏ hơn giá trị thực. 

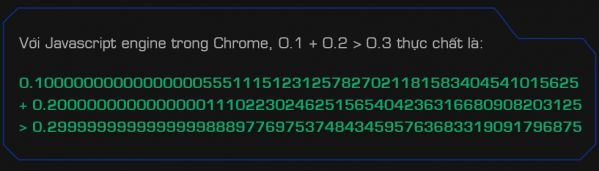
Tương tự, 0.1111111111111117 + 1 có kết quả là 1.1111111111111116 do kết quả của phép tính nhị phân sau khi làm tròn sẽ gần với 1.1111111111111116 hơn là 1.1111111111111117. 

• TẠI SAO KHÔNG THẬP PHÂN

Đọc đến đây bạn có lẽ sẽ đặt ra câu hỏi, vậy tại sao người ta không tạo ra những cỗ máy có thể "nghĩ" theo cách của con người, tức là nghĩ trong hệ số thập phân? Lý do đầu tiên: trong phần lớn trường hợp, chúng ta không cần đến quá nhiều chữ số sau dấu phẩy, nhất là khi các nhà khoa học có những đơn vị đo lường nhỏ hơn cả electron như graviton (1 graviton = 8.9×10−59 kg) hay yocto-met (1 ym = 10^-24 mét). Bộ nhớ máy tính ngày càng lớn có nghĩa rằng con người có thể dùng các đơn vị đo lường rất nhỏ, rồi tính toán trên các giá trị rất lớn.

Lý do thứ hai là các nhà khoa học máy tính thừa đủ thông minh để tạo ra vô số cách "lách" qua giới hạn của máy tính - đơn giản nhất là nhân các số thập phân thành số nguyên rồi áp dấu phẩy sau khi đã tính toán. Phần lớn các ứng dụng sẽ không hé lộ sai số nhị phân cho người dùng cuối: trên Calculator của Windows hay iOS/Android, bạn nhập 0.1 + 0.2 vẫn sẽ cho ra kết quả bằng 0.3.

Nhưng quan trọng hơn hết vẫn là bản chất của máy tính. Chúng sử dụng điện, và dòng điện thì luôn có hai trạng thái bật hoặc tắt. Con người có lẽ có thể tạo ra những cỗ máy có 10 trạng thái, nhưng làm như vậy sẽ khiến các phép tính toán trở nên phức tạp và tiêu tốn tài nguyên hơn rất nhiều. Để tạo ra những điều kỳ diệu như game, VR hay AI, để giải phóng sức mạnh tính toán, chúng ta cần đến hệ nhị phân... 

Dù cái giá phải trả là 0.1 + 0.2 > 0.3.

Theo Trí Thức Trẻ

Devmaster Academy via Genk