Phương trình x³+ y³+ z³ = k là một phương trình 'đẹp' và nổi tiếng. Kể từ năm 1955, các nhà toán học đã sử dụng những máy tính mạnh ...

Phương trình x³+ y³+ z³ = k là một phương trình 'đẹp' và nổi tiếng. Kể từ năm 1955, các nhà toán học đã sử dụng những máy tính mạnh nhất mà họ có để tìm kiếm bộ ba số nguyên thỏa mãn phương trình k = x³ + y³ + z³, tức giải quyết vấn đề: có phân tích được số nguyên k thành "tổng của ba lập phương" hay không? Đôi khi các nghiệm được tìm thấy rất dễ dàng, như với k = 29.

Với k=29, ta thấy ngay nó có vài nghiệm nguyên sau: (1;1;3) và các hoán vị. Tuy nhiên trường hợp k=33 phải mất gần 65 năm người ta mới tìm ra một nghiệm nguyên.

(Nói thêm: Người ta chứng minh được nếu k chia cho 9 mà dư 4 hoặc 5 thì phương trình không có nghiệm nguyên, chẳng hạn với k= 13, k=32.)

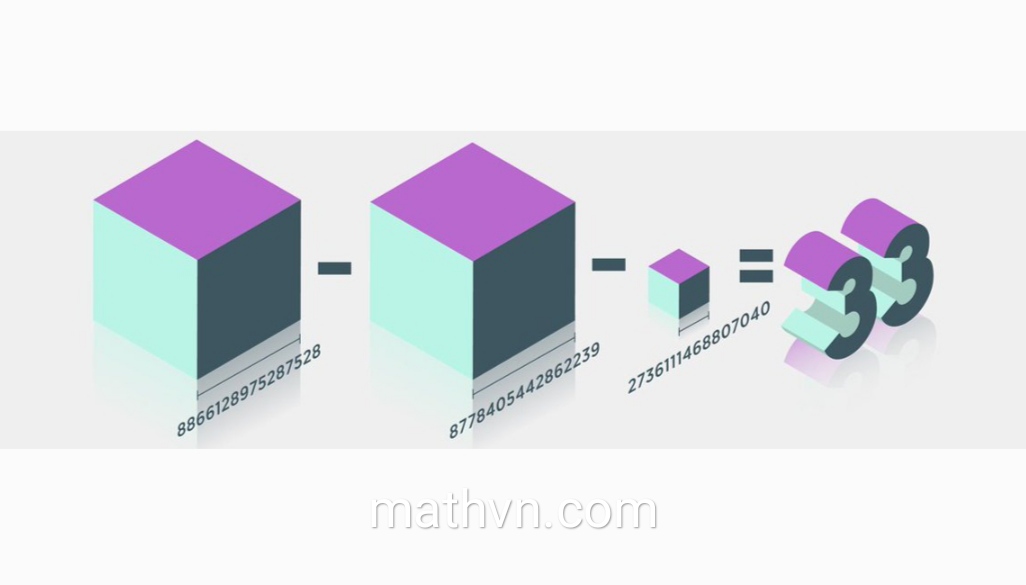
Gần đây, Andrew Booker, một nhà toán học ở  University of Bristol, đã tìm thấy một nghiệm nguyên rất "khủng" - mỗi số gồm 16 chữ số - khi khám phá ra:

(8,866,128,975,287,528)³ + (–8,778,405,442,862,239)³ + (–2,736,111,468,807,040)³ = 33.

Booker đã tìm ra bộ ba số nguyên 16 chữ số kỳ lạ này bằng cách nghĩ ra một thuật toán tìm kiếm mới để chọn chúng ra khỏi hàng nghìn tỷ khả năng. Thuật toán chạy trên một siêu máy tính của trường đại học trong ba tuần liên tiếp. Anh ấy nói rằng anh ấy nghĩ sẽ mất sáu tháng, nhưng một giải pháp “xuất hiện trước khi tôi mong đợi nó.” 

Khi tin tức về nghiệm của Booker xuất hiện trên Internet vào đầu tháng này, các nhà lý thuyết số và những người đam mê toán học đã phát sốt vì phấn khích. Theo một video của Numberphile về khám phá này, Booker thực sự đã nhảy lên vì sung sướng trong văn phòng của mình khi biết được điều đó.
 

Theo Nautilus. Nguồn: MiR Math.